力学を微分積分で超簡単に!その1

どうも〜タクマです!
今回は、微分積分で物理を理解しようということで、大学の範囲になってしまいますが高校生も是非知っておきたいお話をします。
今回のテーマは複数構成にしようと考えているので、是非楽しみにしていてください!
(まず今回の記事では、力学における超基本である位置、速度、加速度についてです。)
この記事で得られることは大きく次の三つです!
1.力学への考え方が大きく変わる
3.数学・物理へのモチベーションが上がる
これから勉強するにあたって本質を知ることになりますので、大きく成長が見込めます
この記事の話を是非友達にも解説してみてください!さらに理解度が上がること間違いなしです!
では、目次をどうぞ!
1.位置、速度、加速度について
2.そもそも微分は、なぜできた?
1.位置、速度、加速度について

まず位置、速度、加速度についてです。
それぞれの定義は次のようになっています。
位置・・・物体が空間のどこにあるかを表す量
速度・・・物体の単位あたりの位置の変位
加速度・・・物体の単位あたりの速度の変化率
このようになっています。もう少し噛み砕いてみてみます。
まず、位置ですがこれはそのままです。物の位置を表すだけです。
しかし、物の位置を人に説明する時にどういう風に説明すれば完璧に伝わるでしょうか
例えば次の虫の位置をどのように伝えますか?

答えは次のように座標を用いることで説明できます。

何が言いたいかというと位置を表すときは、座標を使うということです。
あまり意識しないかもしれないですが、座標を使っているというのは意識しておいて
ください。
次に速度ですが、これも当然の定義です。
位置が変わるということは、動いたということです。当然どれほど時間をかけて位置が変わったかということから単位時間(1秒)あたりの位置の変化となります。
気を付けるべきところは速度は
ベクトル量ということです。
これを理解していない受験生は、本当に多いです💦これを読んでいる人は必ずここでマスターしてください!
では、説明します。
速さというと単に時速5kmとか秒速11mなどの大きさについて言ったものです。
しかし速度はベクトルの量なので単に速さ、つまり大きさだけでなくその向きも考えなければなりません。
このため先ほどの座標が重要になります。
先ほどの図でX軸とY軸に矢印がついています。矢印の向きがプラスの向きつまり正です。
逆はマイナスつまり負です。
これも図に書きましたので確認してみてください!(虫を点で表します)

最後に加速度です。
「加速」と聞くと電車が走り出して加速するといったイメージがあると思います。
そのイメージで大体あっているのですが、もう少し物理的に考えてみます。
速度の時は位置の変位でした。加速度もそれと似ていて速度の変化率です。
例えば、時速5kmから時速60kmになるのに速度が変化していてかつ時間も経っています。この時、加速度が働いているのです。
少し難しい話をすると(難しいので飛ばしてくれても良いですが、知っておくと物理の理解がかなり上がります)
例えばこのような場合はどうでしょうか?
時速5kmから時速5kmへと速度が変化した場合、加速度は働きますか?
この質問への答えはYesです。
キーポイントは「速度が変化した」というところです。
速度の大きさ(速さ)は5km/sのままですが、速度が変化したということは
「向き」が変化したということです。
つまり加速度は速度の変化率であるので加速度が働いてることになります。
これも図を使って説明します。

この話は「等速円運動」でも出てくると思いますので今わからない人も頭の片隅に入れておくぐらいで構いません。
(大学生でも理解していない人は多いです💦)
参考までに実際にセンター試験で出た問題を貼っておきます

かなり良い問題だと思います。
(答えはDMをいただければ解説します!)
次は位置、速度、加速度の関係をみてもっと理解を深めましょう!
2.そもそも微分は、なぜできた?

定義を見ればだいたいわかりますが、今回はグラフや微分積分を使って解説します。
身構えることなく楽しんで読んでみてください。物理がもっと楽しく、面白くなると思います。
ではこのような状況を考えましょう

この情報だけだと始点と終点しかわかっていません。
では、少し情報を足します。図をご覧ください!
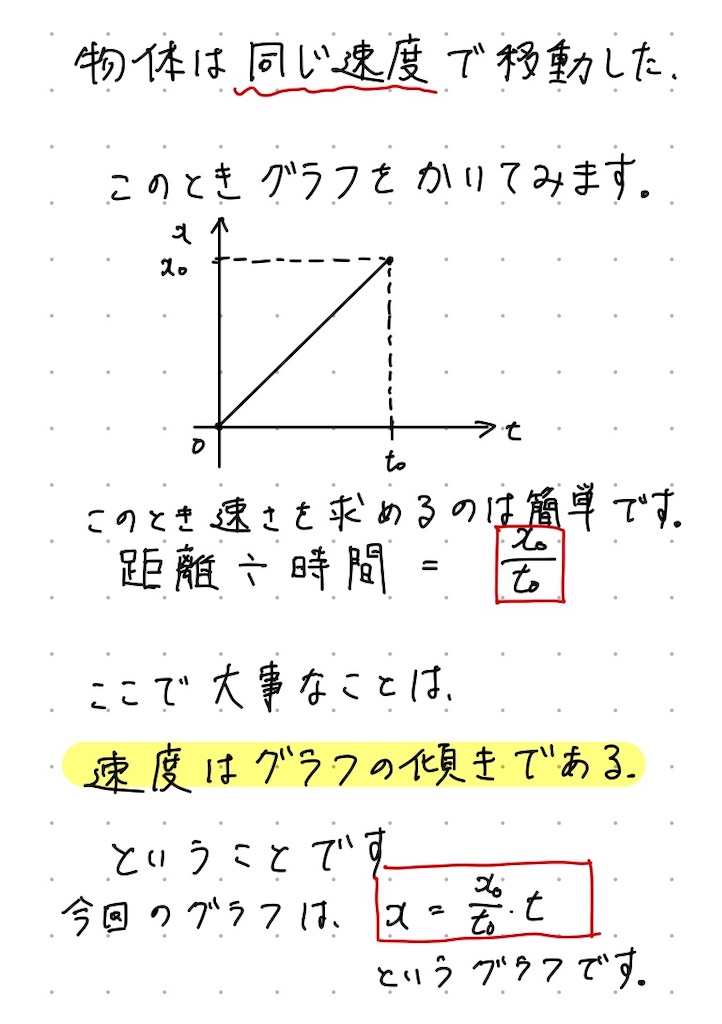
図にもあるように速度は時間と位置のグラフ(x-tグラフ)の傾きを表しています。
では、速度が変化する場合を考えましょう!
グラフが次のようになったとするとどうでしょうか?図をご覧ください。

これは厳密には難しい問題ですね。
先ほどは速度が一定だったので簡単に求められますが今回は刻一刻と速度が変化しています。
では、実際に考えていきましょう!
ここで重要なのが、速度は時間と位置のグラフ(x-tグラフ)の傾き
ということですね!
つまり求めたいものを図にするとこのようになります。
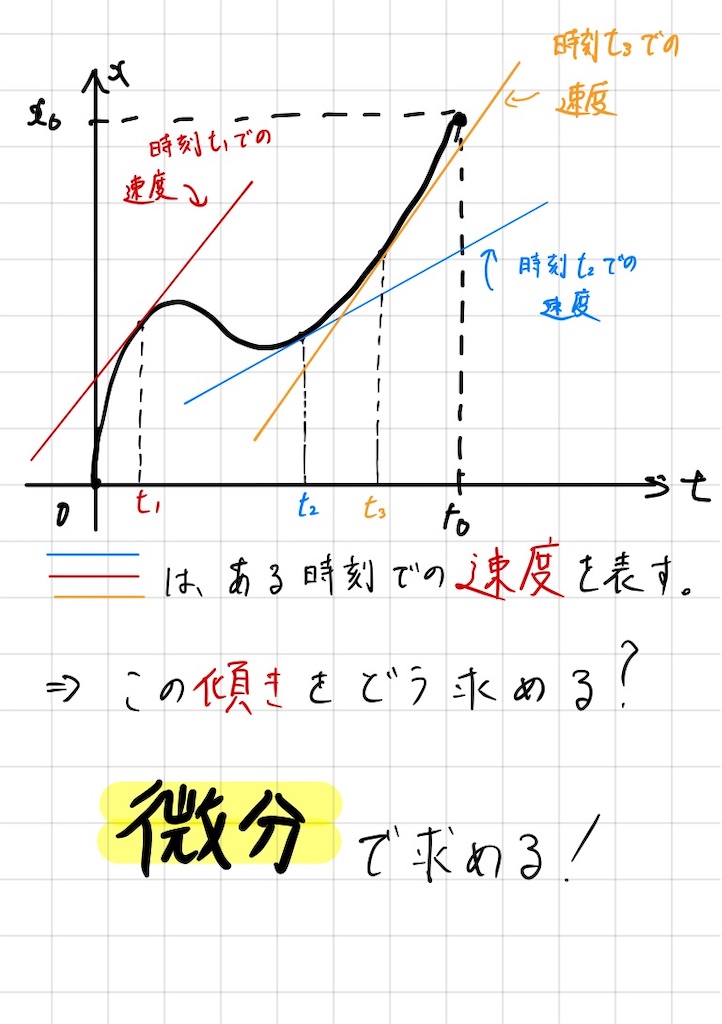
図にも書いているようにこれを求めるのが「微分」です。
数学的には関数の傾きを求めるという作業をしています。
物理的にはこれほど大きな意味を持つため、ニュートンが考え出しました。
なので、「微分は物理から生まれた」と言えるでしょう。
実際に微分を考えていくのは次の記事で書きますのでお楽しみに!
今回の解説で質問があれば、是非DMでお待ちしています!